Optimized Bounding Boxes in XNA

Hi everyone,

for a small project I'm currently working on, I have to deal with 2D collision detection in XNA. There are many great tutorials out there, which I made (and make) extensively use of. However, none of the ones I found deals exactly with the problem I am going to describe right now. Afterwards, I would like to share my solution with you and I hope that some of you might be able to apply it. [UPDATE: See the code in a running XNA 4.0 Example Project here]. Refer to Riemer's wonderful blog, where my solution grounds on. What's more, I'm really looking forward for comments of what you think of my solution :).

Disclaimer
I think this is not an article for absolute beginners. I'm not going to explain the very basics of XNA but I will do my best to explain my bounding box optimization step-by-step.

Problem DescriptionTo illustrate the context, I will use a classical gameplay mechanic as example. Think of a game where objects are randomly spawn at the top of the screen and then fall downwards. The player needs to navigate a player character at the bottom of the screen that catches the falling objects.

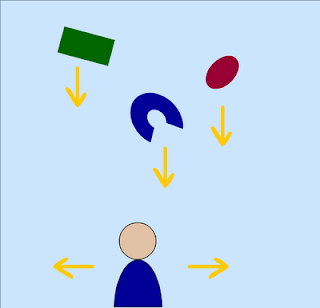
A 2D texture loaded in XNA (sprite) always has fixed bounds which are determined by the graphic file that is loaded. However, it is often necessary to draw such a sprite in a transformed way. Our falling objects, for example, should vary in scale and rotation. Both could be determined randomly.
A simple way to realize collision detection is to use the surrounding rectangles of two objects and check if they intersect. In order to do so we need to adapt the bounding box of a sprite and consider it's position, scale, origin and rotation. This issue has been addressed by Riemer very well and I used his solution (I will round it up a little bit later in the solution section). However, the rotation of objects still bears an issue. Take a look at the following picture.
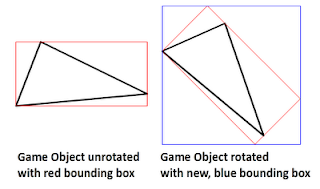On the left side, we see a triangle object unrotated with its red bounding box. Bounding boxes are of type "Rectangle" which is defined by an origin (X and Y coordinates of the upper left corner) and a Width and a Height property. That way, bounding boxes are always axes oriented so that the bounding box of the triangle object on the right side is described by the blue rectangle. My goal was to optimize the bounding box further so that the transparent parts are cropped.
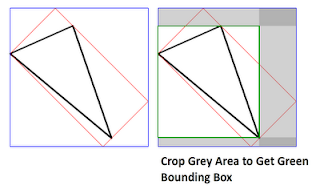In the end, my algorithm works in two steps. First, I use Riemers transformation to calculate the blue bounding box. Then, I crop the transparent bars on left, top, right, and bottom. Let's see how it works!

Solution
Alright, first, it is wise to use a class--commonly named GameObject--which derives from DrawableGameComponent and represents the base class for, well, all drawable game objects in your game. This class stores all information regarding a game object and is responsible for updating and drawing it. For the given context, the necessary fields are:

private Vector2 position;
private Texture2D sprite;
private Vector2 velocity;
private Vector2 origin;
private float rotation;
private float scale;
private Rectangle boundingBox;
private Color[,] pixelData;

Nothing very special here, besides the fact that I use a 2D-Array to store the pixel data of a sprite. It would also work with an 1D-Array, however, I just prefer working with a 2D-array since I think the access by index is easier. We need the pixelData later to be able to find the non-transparent pixels.
This is how I fill the pixelData array when a GameObject-Instance is created:

private Color[,] TextureTo2DArray()
{
Color[] colors1D = new Color[this.sprite.Width *
                            this.sprite.Height];
this.sprite.GetData(colors1D);

Color[,] colors2D = new Color[this.sprite.Width,
                             this.sprite.Height];
for (int x = 0; x < this.sprite.Width; x++)
   for (int y = 0; y < this.sprite.Height; y++)
       colors2D[x, y] =
       colors1D[x + y * this.sprite.Width];

return colors2D;
}

Note that I found this code in another forum or blog, I cannot remember anymore, but it works just fine :).
Alright, now for the meat. Whenever a GameObject is updated, we need to update its bounding box. As I mentioned, I do this in two steps, so I will explain the algorithm in two steps.

Step1: Finding the blue bounding box

protected virtual void UpdateBoundingBox()
{
Matrix toWorldSpace =
   Matrix.CreateTranslation(new Vector3(-this.origin, 0.0f)) *
   Matrix.CreateScale(this.scale) *
   Matrix.CreateRotationZ(this.rotation) *
   Matrix.CreateTranslation(new Vector3(this.position, 0.0f));

this.boundingBox = CalculateTransformedBoundingBox(
   new Rectangle(0, 0, this.sprite.Width, this.sprite.Height),
   toWorldSpace);

// more to come here in step 2
}

private Rectangle CalculateTransformedBoundingBox
(Rectangle local, Matrix toWorldSpace)
{
// Get all four corners in local space
Vector2 leftTop     = new Vector2(local.Left, local.Top);
Vector2 rightTop    = new Vector2(local.Right, local.Top);
Vector2 leftBottom  = new Vector2(local.Left, local.Bottom);
Vector2 rightBottom = new Vector2(local.Right, local.Bottom);

// Transform all four corners into work space
Vector2.Transform(ref leftTop, ref toWorldSpace,
                 out leftTop);
Vector2.Transform(ref rightTop, ref toWorldSpace,
                 out rightTop);
Vector2.Transform(ref leftBottom, ref toWorldSpace,
                 out leftBottom);
Vector2.Transform(ref rightBottom, ref toWorldSpace,
                 out rightBottom);

// Find the minimum and maximum extents of the
// rectangle in world space
Vector2 min = Vector2.Min(Vector2.Min(leftTop, rightTop),
                         Vector2.Min(leftBottom, rightBottom));
Vector2 max = Vector2.Max(Vector2.Max(leftTop, rightTop),
                         Vector2.Max(leftBottom, rightBottom));

// Return that as a rectangle
return new Rectangle((int)min.X, (int)min.Y,
                    (int)(max.X - min.X), (int)(max.Y - min.Y));
}

As I mentioned before the first step is pretty much what Riemer describes here and here. I create a Matrix that transforms the bounds of the game object's sprite from local space to world space. The matrix "toWorldSpace" contains the necessary translations (origin and position), scale and rotation. The method "CalculateTransformedBoundingBox" receives the sprite's bounding box in local space (0,0, width, height) and the transformation matrix. What happens next is that the four edges of the rectangle are transformed one after another. The thus transformed coordinates actually describe the red rectangle that can be seen in the above images for the transformed game object in world space. The following image sums the transformation up that is applied through the matrix "toWorldSpace" to the four coordinates in the lines 26 to 33.
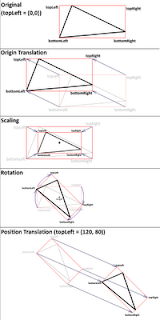Because of the axes-orientation of rectangle objects, however, we cannot describe the rotated rectangle by four coordinates. Instead, we must use the four coordinates to calculate the blue bounding box by the minimum and maximum extends of the red rectangle instead.
Now, how are we able to crop the transparent pixels? This is the bit tricky part. Let's take a look at the code:

Step2: Finding the green bounding box

this.boundingBox = CalculateTransformedBoundingBox(
  new Rectangle(0, 0, this.sprite.Width, this.sprite.Height),
  toWorldSpace);

Matrix boundingBoxTranslation = Matrix.CreateTranslation(
  new Vector3(this.boundingBox.X, this.boundingBox.Y, 0.0f));

Matrix toTextureSpace = boundingBoxTranslation *
                   Matrix.Invert(toWorldSpace);
int orignalWidth = (int)(this.sprite.Width);
int originalHeight = (int)(this.sprite.Height);
int targetWidth = this.boundingBox.Width;
int targetHeight = this.boundingBox.Height;

bool finished = false;
for (int x1 = 0; x1 < targetWidth; x1++)
{
for (int y1 = 0; y1 < targetHeight; y1++)
{
   Vector2 localPosition = new Vector2(x1, y1);
   Vector2 texturePosition = Vector2.Transform(
                             localPosition,
                             toTextureSpace);

   int x2 = (int)texturePosition.X;
   int y2 = (int)texturePosition.Y;

   if ((x2 >= 0) && (x2 < orignalWidth) &&
       (y2 >= 0) && (y2 < originalHeight))
   {
       if (this.pixelData[x2, y2].A > 0)
       {
           this.boundingBox.X =
               (int)Vector2.Transform(
                   localPosition,
                   boundingBoxTranslation).X;
           finished = true;
           break;
       }
   }                                   
}
if (finished)
{
   finished = false;
   break;
}
}

After we calculated the blue bounding box, we have to iterate over the lines and columns of this box and check every position if there is a transparent pixel or not. However, the bounding box actually has no "pixels". Our pixelData is stored in a "local space" representation for the game object's sprite. So, what we do is to first identify the "screen pixel" (world space) by translating from local space to the position of the bounding box. This is achieved by applying the "boundingBoxTranslation" matrix. Secondly, we use the inverted "toWorldSpace" Matrix to find the sprite's corresponding pixel which is actually drawn at the current screen position. We can combine these two steps easily in one matrix by multiplying the bounding box translation matrix with the inverse "toWorldSpace" matrix. Since this is the central part of the algorithm, let us reconsider:

//This matrix translates a coordinate by the position of the
//blue bounding box
Matrix boundingBoxTranslation = Matrix.CreateTranslation(
new Vector3(this.boundingBox.X, this.boundingBox.Y, 0.0f));

// In order to find the coordinates of the texture's pixel that
// is drawn at the screen position, the inverted matrix from
// before can be used
Matrix toTextureSpace = boundingBoxTranslation *
                Matrix.Invert(toWorldSpace);

//...

for(...
for(...
    // coordinate in local space
    Vector2 localPosition = new Vector2(x1, y1);
    // by applying this transformation, we get the
    // cooresponding coordinate of the texture to
    // figure out its pixel's alpha value
    Vector2 texturePosition =
        Vector2.Transform(localPosition, toTextureSpace);

// ...

That way, we get the actual pixel of our texture at the position inside the blue bounding box. Since it might be possible that the found texture position is outside the bounds of our original sprite, we have to consider this. If the texture position is inside, however, we can check the pixels alpha value. In case it is not totally transparent, we found a bound of our new bounding box!
So, the attentive readers might have noticed that the shown nested for-loops iterate column-by-column through the pixels. Thus, the given loops crop the left side of our blue bounding box which in consequence means that we find the optimized X-coordinate. If we did, we can leave both loops and start another run to similarly find the optimized Y-coordinate.

for (int y1 = 0; y1 < targetHeight; y1++)
{
for (int x1 = 0; x1 < targetWidth; x1++)
{
   Vector2 pos1 = new Vector2(x1, y1);
   Vector2 pos2 = Vector2.Transform(pos1, toTextureSpace);

   int x2 = (int)pos2.X;
   int y2 = (int)pos2.Y;

   if ((x2 >= 0) && (x2 < orignalWidth) &&
       (y2 >= 0) && (y2 < originalHeight))
   {
       if (this.pixelData[x2, y2].A > 0)
       {
           this.boundingBox.Y = (int)Vector2.Transform(pos1, boundingBoxTranslation).Y;
           finished = true;
           break;
       }
   }
}
if (finished)
{
   finished = false;
   break;
}
}

Now, we iterate line-by-line, which means that we find our optimized Y-coordinate that way fast. For the sake of completeness, here are the loops to find the width and height afterwards:

for (int x1 = targetWidth-1; x1 >= 0; x1--)
{
for (int y1 = targetHeight-1; y1 >= 0; y1--)
{
   Vector2 pos1 = new Vector2(x1, y1);
   Vector2 pos2 = Vector2.Transform(pos1, toTextureSpace);

   int x2 = (int)pos2.X;
   int y2 = (int)pos2.Y;

   if ((x2 >= 0) && (x2 < orignalWidth) &&
       (y2 >= 0) && (y2 < originalHeight))
   {
       if (this.pixelData[x2, y2].A > 0)
       {
           this.boundingBox.Width = (int)Vector2.Transform(pos1, boundingBoxTranslation).X - this.boundingBox.X;
           finished = true;
           break;
       }
   }
}
if (finished)
{
   finished = false;
   break;
}
}

for (int y1 = targetHeight - 1; y1 >= 0; y1--)
{
for (int x1 = targetWidth - 1; x1 >= 0; x1--)
{
   Vector2 pos1 = new Vector2(x1, y1);
   Vector2 pos2 = Vector2.Transform(pos1, toTextureSpace);

   int x2 = (int)pos2.X;
   int y2 = (int)pos2.Y;

  if ((x2 >= 0) && (x2 < orignalWidth) &&
      (y2 >= 0) && (y2 < originalHeight))
   {
       if (this.pixelData[x2, y2].A > 0)
       {
           this.boundingBox.Height = (int)Vector2.Transform(pos1, boundingBoxTranslation).Y - this.boundingBox.Y;
           finished = true;
           break;
       }
   }
}
if (finished)
{
   break;
}
}

I suppose that's it! Feel free to drop me a comment. I am going to cut the code out of my project to be able to share it with you here the next days. [UPDATE: You find the project here.]

Best,
Robert